Recently I've been thinking way too much about this stuff, so here's a full blog post about it. The aim of this post is to provide a resource other programmers can refer to whenever they have to tackle this problem. There's lots of use-cases for algorithms which generate points or vectors within the limits of a circle - a particle emitter might distribute particles over a circular area; a weapon or special ability might create explosions throughout a target zone; a shotgun's shots spread out in a cone; and so on. So how do you write a speedy, simple, understandable vector-generating function?
Depending on circumstances, you might have different requirements and want to optimise for different things:
Depending on circumstances, you might have different requirements and want to optimise for different things:
- You probably want your points to be uniformly (evenly) distributed across the circle. To verify if an algorithm is outputting uniformly-distributed points, we check the average (mean) distance from the centre of the circle to each point. It should be about (2/3 * radius). This is because half the area of a circle is in its outer third, so when the average distance is (2/3 * radius) you know half the points are in the outer third.
- You may want to minimise calls to the random number generator. Why? Because RNGs can be a bit crap. Certainly the C++ standard library's rand() function is. It might be bad for lots of different reasons. It might have a short period, meaning that it begins to repeat itself after a few thousand calls, which might be a big deal to you. Or it might not be very fast, which is unlikely to be impactful, but this stuff can get pretty weird.
- You might want to avoid using the square-root function. There's a discussion on stackoverflow regarding the speed of sqrt, in which someone says that it is "about 4 times slower than addition using -O2, or about 13 times slower without using -O2." Not huge in the fully-optimised case, but still big enough to add up, and you might be working on hardware where the implementation of sqrt is bad.
- You might want to avoid using many calls to trigonometry functions, because these might be bottlenecks in your code. Sure, you can write sin and cos functions that use a lookup table to speed things along, but maybe you don't want to have to stoop to doing all that work in what should be the age of fast processors. Again, as with rand(), these standard-library should-just-god-damn-work utilities aren't perfect.
- You want to avoid branching in performance-critical code. You can factor comparisons out using smart maths, sometimes, but that involves adding in extra code.
My random number generator
The RandomInRange function I use looks like this:
The RandomInRange function I use looks like this:
// "A Mersenne Twister pseudo-random generator of 32-bit numbers // with a state size of 19937 bits." // Seeded at the beginning of main(). std::mt19937 mt; float RandomInRange(float min, float max) { std::uniform_real_distribution<float> dist(min, max); return dist(mt); }
It's probably the most pleasant-looking version of this function I've ever seen. I'm happy to move beyond using rand() into the bright new world of <random>, even though I'm not sure what the implications are of recreating the distribution object every time the function is called.
Anyway, let's begin!
Anyway, let's begin!
1. The 'naive' algorithm
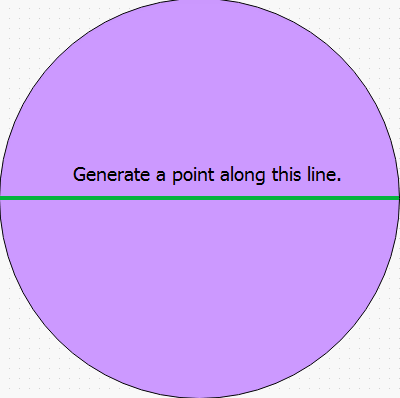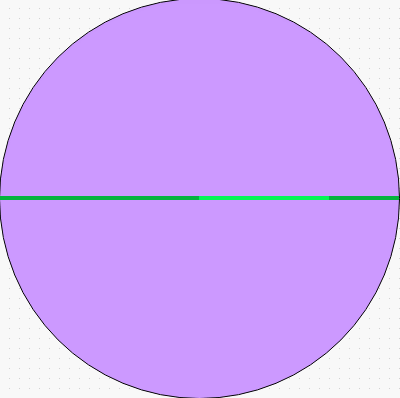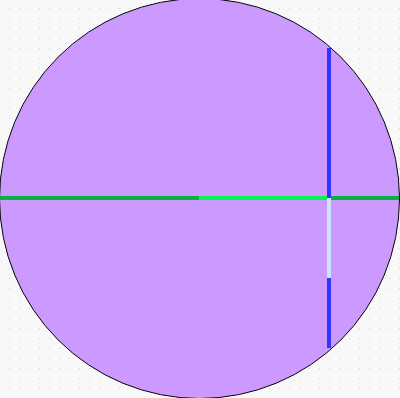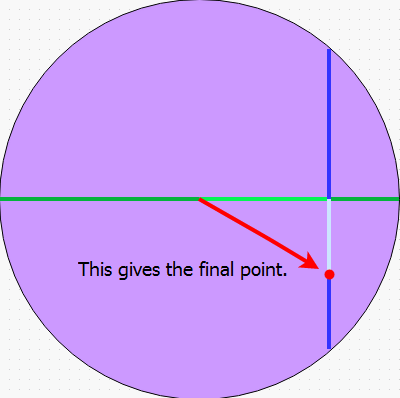
Here we take a basic, intuitive approach. We randomly generate an angle. This gives us a line from the centre of the circle to its circumference. The next random number we generate is used to place the point along this line. Then we use trigonometry to determine the coordinates of the point.
Here we take a basic, intuitive approach. We randomly generate an angle. This gives us a line from the centre of the circle to its circumference. The next random number we generate is used to place the point along this line. Then we use trigonometry to determine the coordinates of the point.
void RandomWithinCircle(float radius, float& x, float& y) { float angle = RandomInRange(0, 2 * PI); float r = RandomInRange(0, radius); x = r * cos(angle); y = r * sin(angle); }
Simple, but naturally flawed. As you can see, it doesn't work if you want a uniform distribution.
The RandomInRange function gives a uniform distribution, so why is this clustering happening?
I mentioned above that the available surface area of a circle gets larger as you go further and further out from the centre, such that half of its area is in its outer third. What this means is that if you just dump points along lines heading out from the centre, the points you dump further out will have much more space for themselves, and those dumped further in will be much more cramped, as you can see. Here, the average distance of points from the centre is 1/2, and this is precisely the problem.
The next two algorithms attempt to solve this problem by skewing the distribution of points towards the outside of the circle, so as to generate uniformly-distributed points.
I mentioned above that the available surface area of a circle gets larger as you go further and further out from the centre, such that half of its area is in its outer third. What this means is that if you just dump points along lines heading out from the centre, the points you dump further out will have much more space for themselves, and those dumped further in will be much more cramped, as you can see. Here, the average distance of points from the centre is 1/2, and this is precisely the problem.
The next two algorithms attempt to solve this problem by skewing the distribution of points towards the outside of the circle, so as to generate uniformly-distributed points.
2. Square, then square root
This takes the same approach, but instead of generating points in the interval [0, radius] we use the interval [0, radius^2]. Then we square-root the result.
This takes the same approach, but instead of generating points in the interval [0, radius] we use the interval [0, radius^2]. Then we square-root the result.
void RandomWithinCircle(float radius, float& x, float& y) { float r = RandomInRange(0, radius*radius); r = sqrtf(r); float angle = RandomInRange(0, 2 * PI); x = r * cos(angle); y = r * sin(angle); }
This works by making larger numbers larger, so that the distribution along each line from centre to circumference is no longer uniform but ever-denser towards the limit. This solves the centre-bias problem by making sure there are more points in the outer areas of the circle and fewer in the central areas.
The algorithm achieves an average point distance of 2/3.
The algorithm achieves an average point distance of 2/3.
3. Folding
This is the technique that Connor showed me that got me thinking about this in the first place. Calling the random function twice and summing the results puts r in the range [0, 2], but if it's greater than 1, the radius of the circle, we 'fold' it back over. For example an r of 1.1 would become 0.9. An r of 1.9 would become 0.1.
This is the technique that Connor showed me that got me thinking about this in the first place. Calling the random function twice and summing the results puts r in the range [0, 2], but if it's greater than 1, the radius of the circle, we 'fold' it back over. For example an r of 1.1 would become 0.9. An r of 1.9 would become 0.1.
void RandomWithinCircle(float radius, float& x, float& y) { float r = RandomInRange(0.0f, 1.0f) + RandomInRange(0.0f, 1.0f); if (r > 1.0f) { r = 2.0f - r; } r *= radius; float angle = RandomInRange(0.0f, 2.0f * PI); x = r * cos(angle); y = r * sin(angle); }
This gives a uniform distribution:
But how?
The distribution that RandomInRange(0, 1) + RandomInRange(0, 1) gives is weighted towards its centre, that is, 1. Folding this distribution over balances the distribution of points away from the centre of the circle and closer to the edge. You might get a better explanation here.
The distribution that RandomInRange(0, 1) + RandomInRange(0, 1) gives is weighted towards its centre, that is, 1. Folding this distribution over balances the distribution of points away from the centre of the circle and closer to the edge. You might get a better explanation here.
4. Triangulation
Generate 2 numbers a and b, ensuring that a is smaller than b. Calculate the ratio a/b. This ratio determines the angle used. b determines how far out along the radius the point is placed. I found the algorithm here.
Generate 2 numbers a and b, ensuring that a is smaller than b. Calculate the ratio a/b. This ratio determines the angle used. b determines how far out along the radius the point is placed. I found the algorithm here.
void RandomWithinCircle(float radius, float& x, float& y) { float a = RandomInRange(0.f, 1.f); float b = RandomInRange(0.f, 1.f); if (b < a) { // swap them float temp = a; a = b; b = temp; } x = b * radius * cos(2.f * PI * a/b); y = b * radius * sin(2.f * PI * a/b); }
It gives a uniform distribution, so I won't share a gif of it in action because it looks the exact same as the previous two.
5. My algorithm (honourable mention)
I came up with this pretty quickly without thinking about it much. It doesn't quite work.
I came up with this pretty quickly without thinking about it much. It doesn't quite work.
void RandomWithinCircle(float radius, float& x, float& y) { x = RandomInRange(-radius, radius); float angle = acos(x/radius); float lim = radius * sin(angle); y = RandomInRange(-lim, lim); }
As you can see, points end up clustered towards the right and left-hand edges of the circle. This is because lim becomes smaller and smaller the larger x is (in terms of magnitude), so there's less and less space to fit points into. To fix this problem I'd have to skew the distribution of x back, closer to zero - I think maybe a clamped normal distribution of some kind would do it?
6. Point-rejection (dishonourable mention)
Generate points inside the square of width d and reject the ones that lie outside the circle of diameter d.
Not good. You shouldn't do this because the algorithm will take a random amount of time to complete, which is completely useless in almost every situation.
Generate points inside the square of width d and reject the ones that lie outside the circle of diameter d.
Not good. You shouldn't do this because the algorithm will take a random amount of time to complete, which is completely useless in almost every situation.




 RSS Feed
RSS Feed
